零基础SICP 11

零基础SICP 11

符号数据和符号求导

沈浪熊猫儿

MathAgape

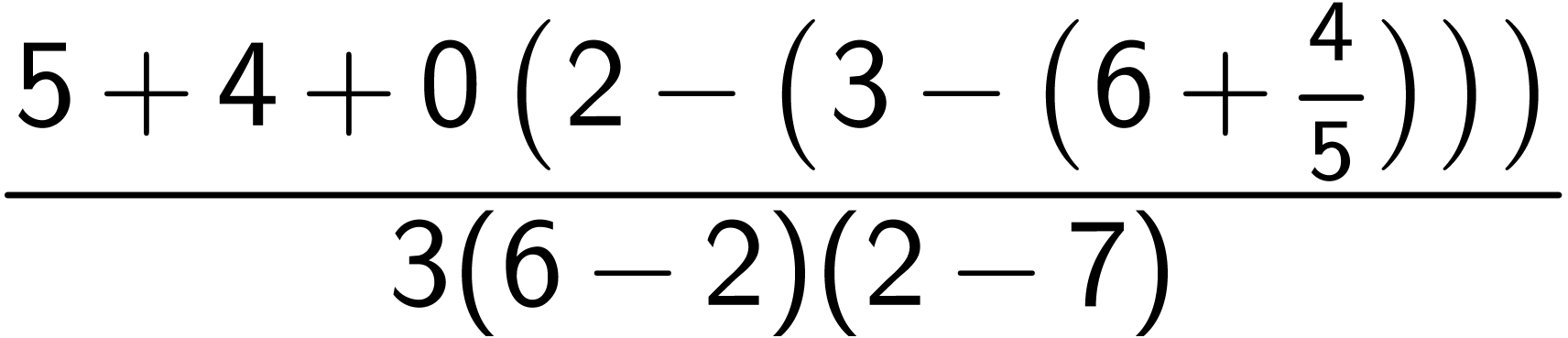
零基础SICP：第11课

数据抽象导引	Introduction to Data Abstraction

层次性数据和闭包性质	Hierarchical Data and the Closure Property

符号数据	Symbolic Data
引号	Quotation
实例：符号求导	Example: Symbolic Differentiation

回顾：通过定义一组逻辑自洽的选择函数和构造函数，定义数据。

回顾：语法糖衣

特殊形式不符合应用序求值，比如define，cond，if（零基础SICP第一讲的内容）

>	(define (myabs x) (if (> x 0) x (- x)))

>	(myabs -1)

>	((lambda (x) (if (> x 0) x (- x))) -1)

-1

(- 1)

(list? )

即使我们的Scheme解释器不支持-1，define，我们也可以使用更加繁琐的语法来表示同样的含义。语法糖衣并没有给我们带来新的能力，但能帮助我们简化代码。

利用宏编程的特性，我们可以自定义语法糖衣。

定义符号数据—构造函数quote

'是一种语法糖衣，如果没有'，也可以使用quote。Scala里面也有符号数据。SRFI-1 List

'a

(quote a)

''a

>	(quote (quote a))

'1

>	(eq? 1 (quote 1))

'#t

>	(eq? #t ‘#t)

'+

>	(eq? + '+)

''

字面量（literally）在引用（两次引用？）之后，还是字面量。符号在引用之后，则变成了符号数据。

定义符号数据—选择函数unquote

,是一种语法糖衣，如果没有,，也可以使用unquote。unquote只能在‘（quasiquote）下使用。

>	(define a 1)

'a

(quote a)

‘,a

>	(quasiquote (unquote a))

试译：quote为引用，unquote为解引用，quasiquote为准引用。' 是引号，, 是解引号，‘ 是准引号。

定义符号数据—参数为列表的构造函数

'(a b c)

>	(list 'a 'b 'c)

>	'(a b (c d))

>	(list 'a 'b (list 'c 'd))

'(+ 1 2)

' ; quote

‘ ; quasiquote

, ; unquote

定义符号数据—在列表中理解选择函数

'(+ a 1)

>	(define a 4)

>	‘(+ ,(+ a 1) 1)

‘(+ ,a 1)

>	(eval ‘(+ ,a 1))

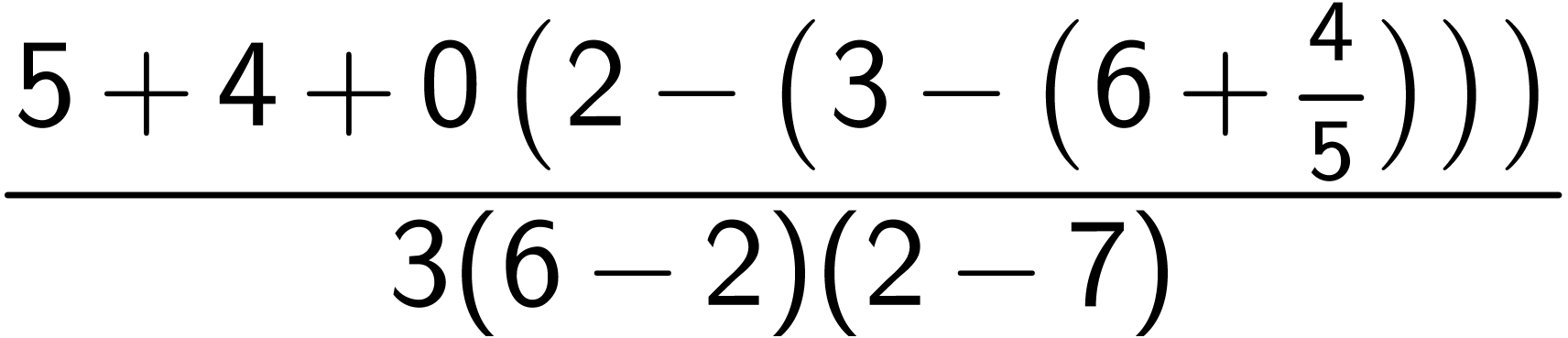
用符号数据可以延迟计算过程。延迟计算过程，可以避免无效计算和重复计算。

>	(define 分子 ‘(+ 5 4 (- 2 (- 3 (+ 6 (/ 4 5))))))

>	(define 分母 ‘(* 3 (- 6 2) (- 2 7)))

>	‘(/ ,分子 ,分母)

>	(eval ‘(/ ,分子 ,分母))

（这个例子来自于《零基础SICP》第2.1课 00:12:00）

符号求导

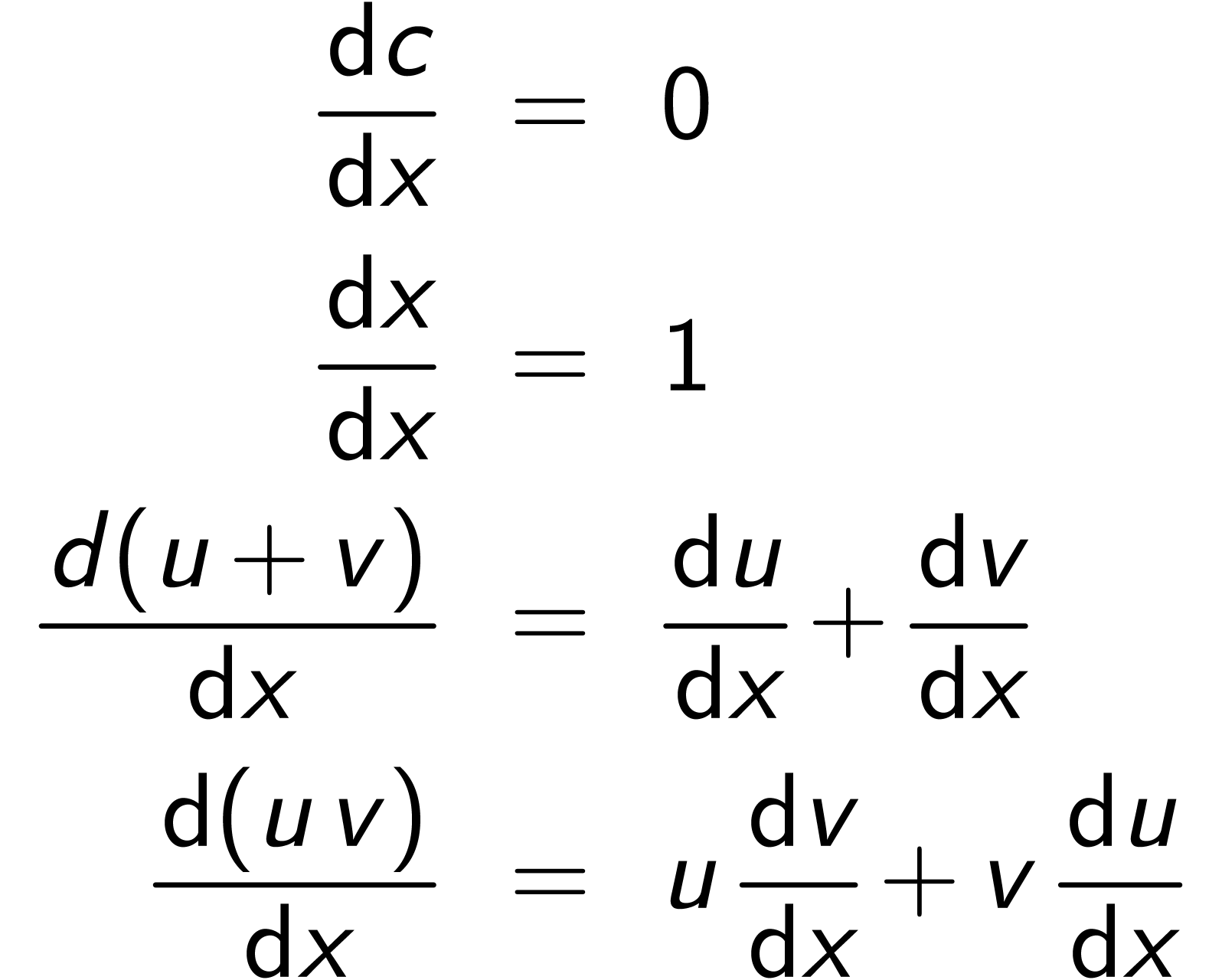
注意. 是一个常数或者是一个和无关的变量。

符号求导—应用

>	(deriv '(+ x 3) 'x)

>	(deriv '(* x y) 'x)

>	(deriv '(* (* x y) (+ x 3)) 'x)

Maxima 5.46.0 https://maxima.sourceforge.io using Lisp GNU Common Lisp (GCL) GCL 2.6.14 git tag Version_2_6_15pre3 Distributed under the GNU Public License. See the file COPYING. Dedicated to the memory of William Schelter. The function bug_report() provides bug reporting information.

(%i4)

diff()

(%i5)

diff(,x)

(%i6)

diff(,x)

(%i7)

符号求导—实现

(define (deriv exp var)
  (cond ((number? exp) 0)
        ((variable? exp)
         (if (same-variable? exp var) 1 0))
        ((sum? exp)
         (make-sum (deriv (addend exp) var)
                   (deriv (augend exp) var)))
        ((product? exp)
         (make-sum
           (make-product (multiplier exp)
                         (deriv (multiplicand exp) var))
           (make-product (deriv (multiplier exp) var)
                         (multiplicand exp))))
        (else
         (error "unknown expression type -- DERIV" exp))))

deriv

符号求导—基础函数

>	(define (variable? x) (symbol? x)) ; 判断x是不是变量

>	(define (same-variable? v1 v2) ; v1和v2是不是同一个变量 (and (variable? v1) (variable? v2) (eq? v1 v2)))

>	(define (make-sum a1 a2) (list '+ a1 a2)) ;

>	(define (make-product m1 m2) (list '* m1 m2))

>	(define (sum? x) (and (pair? x) (eq? (car x) '+))) ; x是和式么？

>	(define (addend s) (cadr s)) ; s的被加数（加号左边那个数）

>	(define (augend s) (caddr s)) ; s的加数（加号右边那个数）

>	(define (product? x) ; x是否是一个乘式 (and (pair? x) (eq? (car x) '*)))

>	(define (multiplier p) (cadr p)) ; p的被乘数（乘号左边）

>	(define (multiplicand p) (caddr p)) ; p的乘数（乘号右边）

小结

回顾语法糖衣这个概念
针对原语表达式定义符号数据
针对复合表达式定义符号数据
理解符号数据：实现延迟计算
应用符号数据：符号求导