零基础SICP 10
函数式编程三板斧

沈浪熊猫儿

MathAgape

零基础SICP：第10课

数据抽象导引

Introduction to Data Abstraction

实例：有理数的算术运算

Example: Arithmetic Operations for Rational Numbers

抽象层级

Abstraction Barriers

数据意味着什么

What Is Meant by Data?

层次性数据和[闭包性质]

Hierarchical Data and the Closure Property

序列的表示

Representing Sequences

层次性结构

Hierarchical Structures

序列作为一种约定的接口

Sequences as Conventional Interfaces

利用函数式编程三板斧（映射/过滤/折叠）和衍生算子描述数据处理逻辑。

定义数据：list

通过定义一组逻辑自洽的选择函数和构造函数，定义数据。

构造器 

> 
(list 1 2 3 4)

(1 2 3 4) 

> 
(cons 5 (list 1 2 3 4))
 

> 
()
 

> 

              

            

          

        

      

    

    

      选择器
    

    

      

        

          

            

              

                
> 

                
(car (list 1 2 3 4))

              

            

          

        

      

    

    

      

        

          

            

              

                
> 

                
(cdr (list 1 2 3 4))

              

            

          

        

      

    

    

      

        

          

            

              

                
> 

                
(cadr (list 1 2 3 4))

              

            

          

        

      

    

    

      

        

          

            

              

                
> 

                
(list-ref (list 1 2 3 4) 3)

              

            

          

        

      

    

    

      

        

          

            

              

                
> 

                

              

            

          

        

      

    

    

      性质
    

    

      

        

          

            

              

                
> 

                
(list? (list 1))

              

            

          

        

      

    

    

      

        

          

            

              

                
> 

                
(list? 1)

              

            

          

        

      

    

    

      

        

          

            

              

                
> 

                
(eq? () ())

              

            

          

        

      

    

    

      

        

          

            

              

                
> 

                
(eq? () (list 1))

              

            

          

        

      

    

    

      

        

          

            

              

                
> 

                
(null? ())

              

            

          

        

      

    

    

      

        

          

            

              

                
> 

                
(length (list 1 2 3 4))

              

            

          

        

      

    

    

      

        

          

            三板斧之映射：map
          

        

          

            
          

        

      

    

    

      map是S7
      Scheme的内置函数
    

    

      

        

          

            

              

                
> 

                
(define (square x) (* x x))

              

            

          

        

      

    

    

      

        

          

            

              
> 

              
(map square (list 1 2 3 4 5))

            

          

        

      

    

    

      

        

          

            

              
> 

              
(map (lambda (x) (* x x)) (list 1 2 3 4 5))

            

          

        

      

    

    

      

        

          

            

              
> 

              
(map (lambda (x) (+ x 1)) (list 1 2 3 4 5))

            

          

        

      

    

    

      

        

          

            

              
> 

              
(map (lambda (x) (append x "@liii.pro")) (list "da" "nian"))

            

          

        

      

    

    

      

        

          

            

              
> 

              
(map odd? (list 1 2 3 4 5))

            

          

        

      

    

    

      

        

          

            

              

                
> 

                

              

            

          

        

      

    

    

      

        

          

            三板斧之过滤：filter
          

        

          

            
          

        

      

    

    

      SRFI-1: List Library中定义了filter，我们需要自己实现
    

    

      实现
    

    

      

        

          

            

              

                
> 

                
(define (filter pred? seq)
  (cond
   ((null? seq) ())
   ((pred? (car seq))
    (cons (car seq)
          (filter pred? (cdr seq))))
   (else (filter pred? (cdr seq)))))

              

            

          

        

      

    

    

      

        

          

            

              

                

                  filter
                

              

            

          

        

      

    

    

      应用
    

    

      

        

          

            

              

                
> 

                
(filter odd? (list 1 2 3 4 5))

              

            

          

        

      

    

    

      

        

          

            

              

                
> 

                
(filter even? (list 1 2 3 4 5))

              

            

          

        

      

    

    

      

        

          

            

              

                
> 

                
(filter (lambda (x) (> x 3)) '(1 3 5))

              

            

          

        

      

    

    

      

        

          

            

              

                
> 

                
(filter (lambda (x) (= x 3)) ‘(1 3 5))

              

            

          

        

      

    

    

      

        

          

            

              

                
> 

                
(filter (lambda (x) (> x 20))
 (map (lambda (x) (* x x))
  (list 1 2 3 4 5 6)))

              

            

          

        

      

    

    

      

        

          

            

              

                
> 

                

              

            

          

        

      

    

    

      

        

          

            三板斧之折叠：fold和fold-right
          

        

          

            
          

        

      

    

    

      SRFI-1: List Library中定义了fold，我们需要自己实现
    

    

      实现
    

    

      

        

          

            

              

                
> 

                
(define (fold op initial seq)
 (if (null? seq)
  initial
  (fold op
        (op (car seq) initial)
        (cdr seq))))

              

            

          

        

      

    

    

      

        

          

            

              

                
> 

                
(define (fold-right op initial seq)
 (if (null? seq)
  initial
  (op (car seq)
      (fold-right op
                  initial
                  (cdr seq)))))

              

            

          

        

      

    

    

      应用
    

    

      

        

          

            

              

                
> 

                
(fold + 0 (list 1 2 3 4))

              

            

          

        

      

    

    

      

        

          

            

              

                

                  10
                

              

            

          

        

      

    

    

      

        

          

            

              

                
> 

                
(fold-right + 0 (list 1 2 3 4))

              

            

          

        

      

    

    

      

        

          

            

              

                

                  10
                

              

            

          

        

      

    

    

      

        

          

            

              

                
> 

                
(fold cons () (list 1 2 3 4))

              

            

          

        

      

    

    

      

        

          

            

              

                

                  (4 3 2 1)
                

              

            

          

        

      

    

    

      

        

          

            

              

                
> 

                
(fold-right cons () (list 1 2 3 4))

              

            

          

        

      

    

    

      

        

          

            

              

                

                  (1 2 3 4)
                

              

            

          

        

      

    

    

      

        

          

            

              

                
> 

                

              

            

          

        

      

    

    

      

        

          

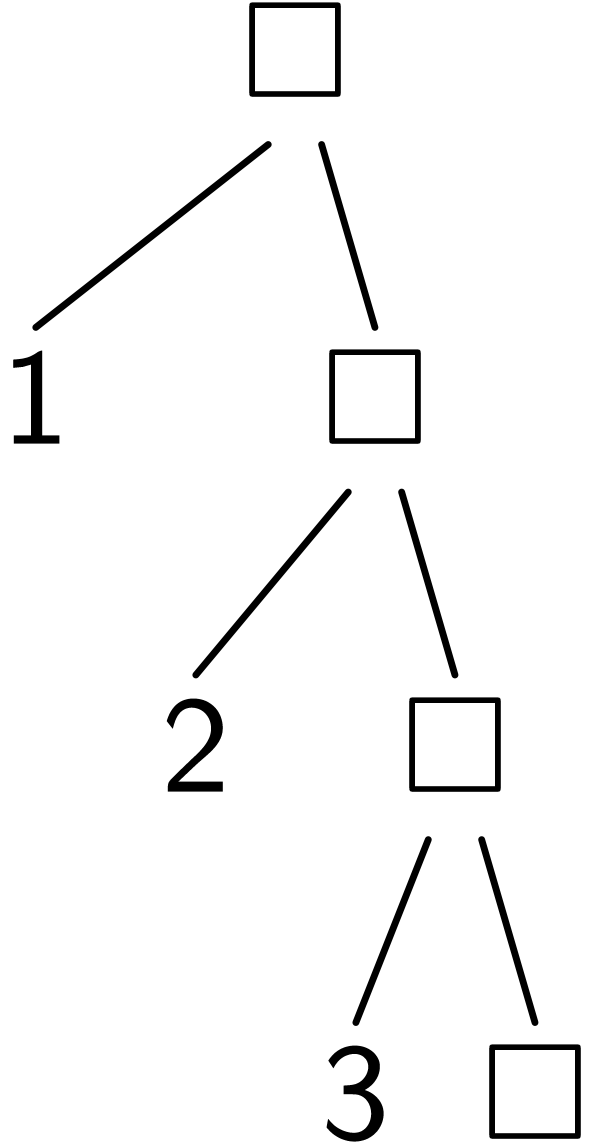
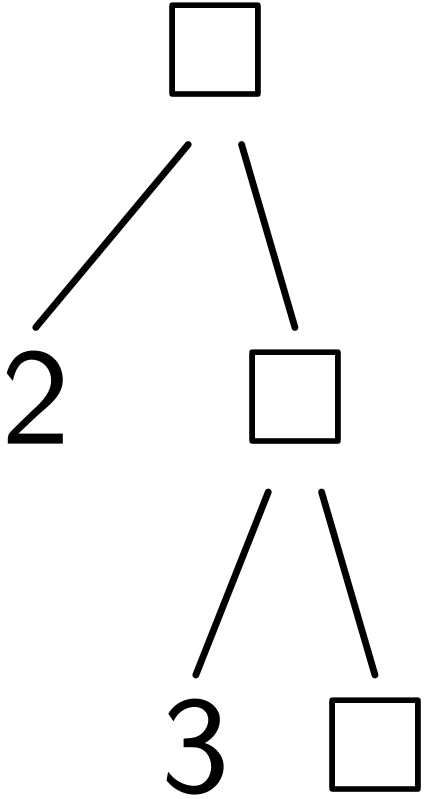
            理解左折叠fold
          

        

          

            
          

        

      

    

    

      通过可视化理解(fold
      cons () (list 1 2 3))
    

    

      

        

          

            ; Step 0
          

        

      

    

    

      

        

          

            (fold cons 
          

        

      

    

    

      

        

          

              ()
          

        

      

    

    

      

        

          

             )
          

        

      

    

    

      

        

          

            ; Step 1
          

        

      

    

    

      

        

          

            (fold cons 
          

        

      

    

    

      

        

          

              
          

        

      

    

    

      

        

          

            
          

        

      

    

    

      

        

          

             )
          

        

      

    

    

      

        

          

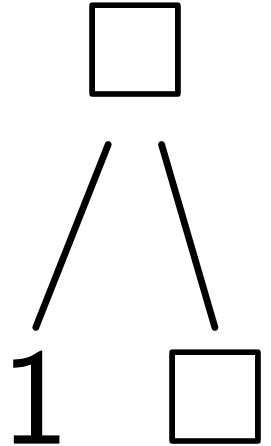
            ; Step 2
          

        

      

    

    

      

        

          

            (fold cons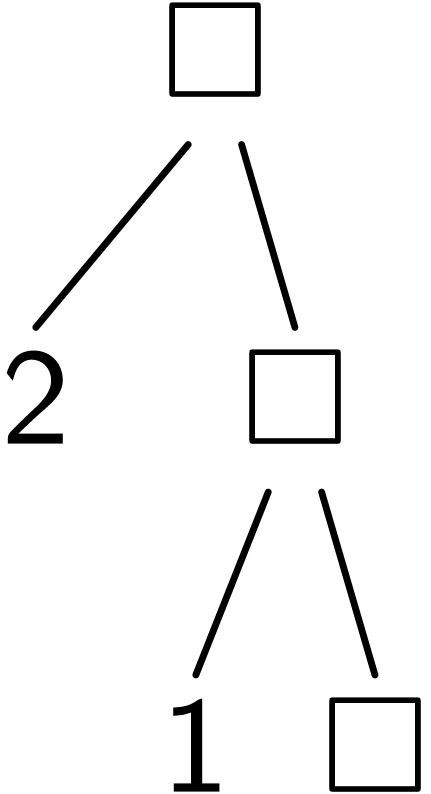  
          

        

      

    

    

      

        

          

            
          

        

      

    

    

      

        

          

              )
          

        

      

    

    

      

        

          

            
          

        

      

    

    

      

        

          

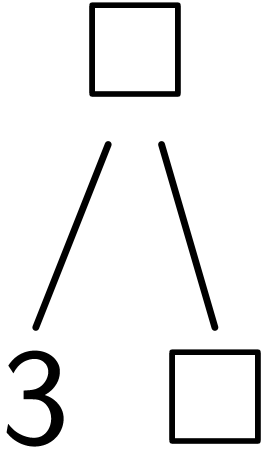            ; Step 3
          

        

      

    

    

      

        

          

            (fold cons  ())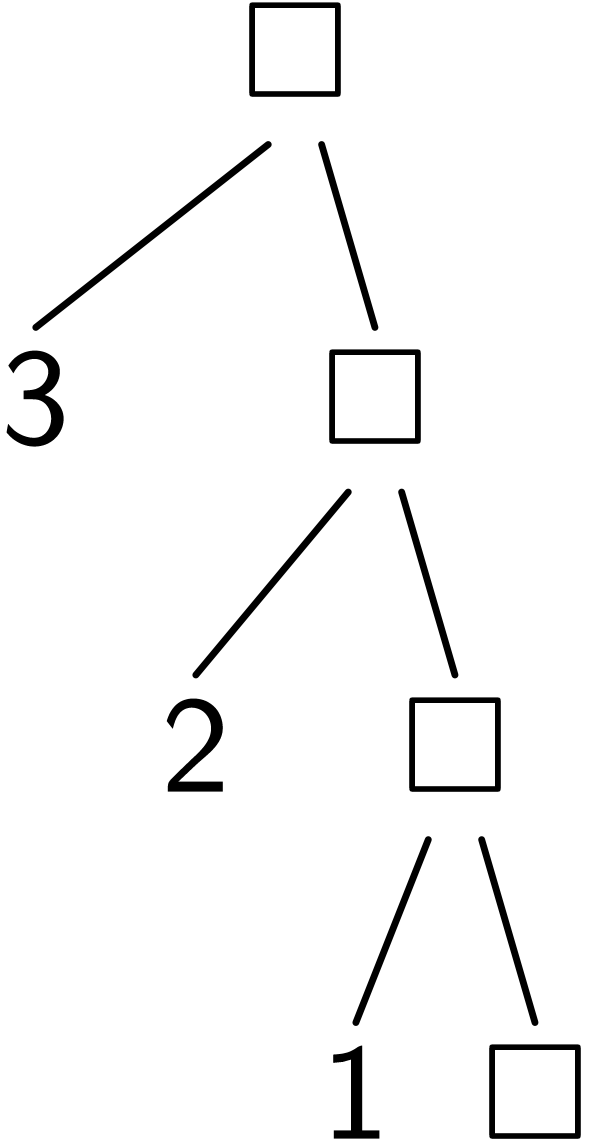
          

        

      

    

    

      

        

          

            理解右折叠fold-right步骤0-1
          

        

          

            
          

        

      

    

    

      通过可视化理解(fold-right
      cons () (list 1 2 3))
    

    

      

        

          

            ; Step 0
          

        

      

    

    

      

        

          

            (fold-right cons () )
          

        

      

    

    

      

        

          

            ; Step 1
          

        

      

    

    

      

        

          

            (cons 1
          

        

      

    

    

      

        

          

             (fold-right cons () )))
          

        

      

    

    

      

        

          

            
          

        

      

    

    

      

        

          

            
          

        

      

    

    

      

        

          

            理解右折叠fold-right步骤2-3
          

        

          

            
          

        

      

    

    

      通过可视化理解(fold-right
      cons () (list 1 2 3))
    

    

      

        

          

            ; Step 2
          

        

      

    

    

      

        

          

            (cons 1
          

        

      

    

    

      

        

          

             (cons 2
          

        

      

    

    

      

        

          

              (fold-right cons () )))
          

        

      

    

    

      

        

          

            
          

        

      

    

    

      

        

          

            
          

        

      

    

    

      

        

          

            
          

        

      

    

    

      

        

          

            
          

        

      

    

    

      

        

          

            
          

        

      

    

    

      

        

          

            
          

        

      

    

    

      

        

          

            ; Step 3
          

        

      

    

    

      

        

          

            (cons 1 (cons 2 (cons 3 ()))))
          

        

      

    

    

      

        

          

            
          

        

      

    

    

      

        

          

            
          

        

      

    

    

      

        

          

            衍生算子：flatmap
          

        

          

            
          

        

      

    

    

      

        

          

            

              

                
> 

                
(define (flatmap f seq)
  (fold-right append () (map f seq)))

              

            

          

        

      

    

    

      

        

          

            

              

                flatmap
              

            

          

        

      

    

    

      

        

          

            

              
> 

              
(flatmap (lambda (x) (list x x)) (list 1 2 3 4))

            

          

        

      

    

    

      

        

          

            

              

                (1 1 2 2 3 3 4 4)
              

            

          

        

      

    

    

      

        

          

            

              
> 

              
(map (lambda (x) (list x x)) (list 1 2 3 4))

            

          

        

      

    

    

      

        

          

            

              

                ((1 1) (2 2) (3 3) (4 4))
              

            

          

        

      

    

    

      

        

          

            

              

                
> 

                

              

            

          

        

      

    

    

      
    

    

      
    

    

      

        

          

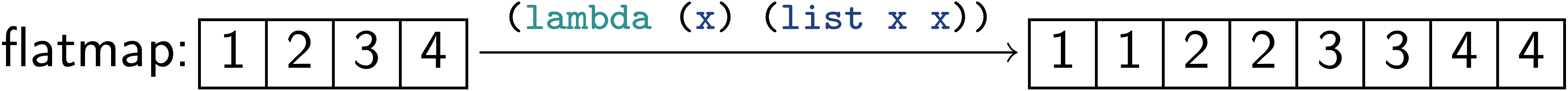
            衍生算子：flatmap的应用
          

        

          

            
          

        

      

    

    

      

        

          

            

              

                
> 

                
(define (remove item sequence)
  (filter (lambda (x) (not (= x item)))
          sequence))

              

            

          

        

      

    

    

      

        

          

            

              
> 

              
(define (permutations s)
  (if (null? s)                   ; empty set?
      (list ())                   ; sequence containing empty set
      (flatmap (lambda (x)
                 (map (lambda (p) (cons x p))
                      (permutations (remove x s))))
               s)))

            

          

        

      

    

    

      

        

          

            

              
> 

              
(permutations (list 1 2 3))

            

          

        

      

    

    

      

        

          

            

              

                ((1 2 3) (1 3 2) (2 1 3) (2 3 1) (3 1 2) (3 2 1))
              

            

          

        

      

    

    

      

        

          

            

              

                
> 

                

              

            

          

        

      

    

    

      

        

          

            总结