零基础SICP 08
有理数的数据抽象

沈浪熊猫儿

MathAgape

零基础SICP：第8课

数据抽象导引

Introduction to Data Abstraction

实例：有理数的算术运算

Example: Arithmetic Operations for Rational Numbers

抽象层级

Abstraction Barriers

数据意味着什么

What Is Meant by Data?

编程的基本原理是对数据和计算的组合和抽象

有理数与分式

预定义函数：分式、分式显、分子、分母 

Scheme] 
(define 二分之一 (分式 1 2))
 

Scheme] 
(define 三分之一 (分式 1 3))
 

Scheme] 
(分子 二分之一)

1 

Scheme] 
(分母 二分之一)

2 

Scheme] 
(分式显 三分之一)

1
3 

Scheme] 
(分式显 二分之一)

1
2

Scheme] 

              

            

          

        

      

    

    
    

      

        

          

            有理数的算术运算
          

        

          

            
          

        

      

    

    

      

        

          

            

              

                
Scheme] 

                
(分式显 (分式加 二分之一 三分之一))

              

            

          

        

      

    

    

      

        

          

            

              

                

                  

                    5
                  

                  

                    6
                  

                

              

            

          

        

      

    

    

      

        

          

            

              

                
Scheme] 

                
(分式显 (分式减 二分之一 三分之一))

              

            

          

        

      

    

    

      

        

          

            

              

                

                  

                    1
                  

                  

                    6
                  

                

              

            

          

        

      

    

    

      

        

          

            

              

                
Scheme] 

                
(分式显 (分式乘 二分之一 三分之一))

              

            

          

        

      

    

    

      

        

          

            

              

                

                  

                    1
                  

                  

                    6
                  

                

              

            

          

        

      

    

    

      

        

          

            

              

                
Scheme] 

                
(分式显 (分式除 二分之一 三分之一))

              

            

          

        

      

    

    

      

        

          

            

              

                

                  

                    3
                  

                  

                    2
                  

                

              

            

          

        

      

    

    

      

        

          

            

              

                Scheme] 
                

              

            

          

        

      

    

    

      算术运算函数：分式加,分式减,分式乘,分式除
    

    

      

        

          

            分式加
          

        

          

            
          

        

      

    

    

      
    

    

      

        

          

            

              

                
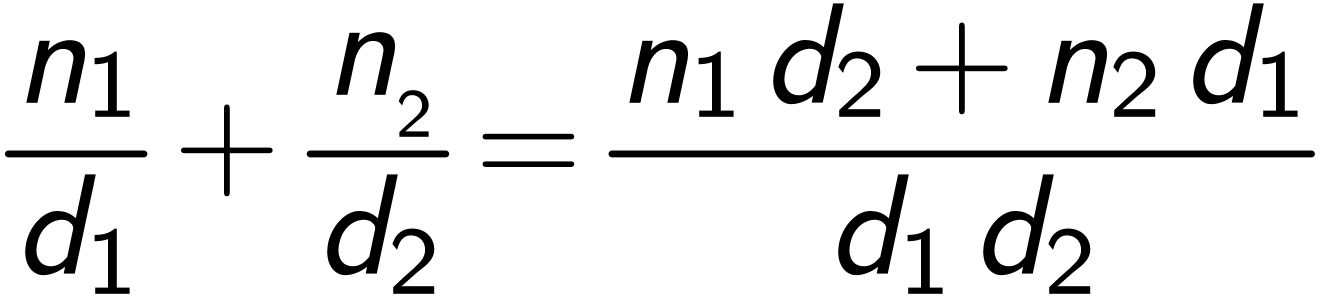
Scheme] 

                
(define (分式加 x y)
  (let* ((n1 (分子 x))
         (d1 (分母 x))
         (n2 (分子 y))
         (d2 (分母 y)))
    (分式 (+ (* n1 d2) (* n2 d1))
          (* d1 d2))))

              

            

          

        

      

    

    

      

        

          

            

              

                分式加
              

            

          

        

      

    

    

      

        

          

            

              
Scheme] 

              
(分式显 (分式加 (分式 1 2) (分式 1 4)))

            

          

        

      

    

    

      

        

          

            

              

                Scheme] 
                

              

            

          

        

      

    

    

      

        

          

            抽象层级
          

        

          

            
          

        

      

    

    

      将接口与实现的隔离
    

    
    
    

      
    

    

      

        

          

            有序对的抽象
          

        

          

            
          

        

      

    

    

      

        

          pair
        

        

          

            构造器：提供两个参数，构造一个有序对
          

        

      

      

        

          pair.x1
        

        

          

            选择器：有序对中的第一个元素
          

        

      

      

        

          pair.x2
        

        

          

            选择器：有序对中的第二个元素
          

        

      

    

    

      

        

          

            

              

                
Scheme] 

                
(define (pair x1 x2) (cons x1 x2))

              

            

          

        

      

    

    

      

        

          

            

              
Scheme] 

              
(define (pair.x1 p) (car p))

            

          

        

      

    

    

      

        

          

            

              
Scheme] 

              
(define (pair.x2 p) (cdr p))

            

          

        

      

    

    

      

        

          

            

              
Scheme] 

              
(pair 1 2)

            

          

        

      

    

    

      

        

          

            

              
Scheme] 

              
(pair.x1 (pair 3 4))

            

          

        

      

    

    

      

        

          

            

              
Scheme] 

              
(pair.x2 (pair "父亲" "母亲"))

            

          

        

      

    

    

      

        

          

            

              

                Scheme] 
                

              

            

          

        

      

    

    

      

        

          

            基础数据结构：链表
          

        

          

            
          

        

      

    

    

      

        

          ()
        

        

          

            构造器：表示空链表
          

        

      

      

        

          cons
        

        

          

            构造器：提供一个元素和一个链表，将两者组合成链表。
          

        

      

      

        

          car
        

        

          

            选择器：取出链表头部的元素。
          

        

      

      

        

          cdr
        

        

          

            选择器：移除链表头部之后，剩下的元素按照原来的顺序组合成的链表。
          

        

      

      

        

          list
        

        

          

            构造器：提供一组元素，可以将这一组元素组合成链表。
          

        

      

    

    

      

        

          

            

              

                
Scheme] 

                
(list 1 2 3 4) # (cons 1 (cons 2 (cons 3 (cons 4 ()))))

              

            

          

        

      

    

    

      

        

          

            

              
Scheme] 

              
(car (list 1 2 3 4))

            

          

        

      

    

    

      

        

          

            

              
Scheme] 

              
(cdr (list 1 2 3 4))

            

          

        

      

    

    

      

        

          

            

              
Scheme] 

              
(car (list ))

            

          

        

      

    

    

      

        

          

            

              
Scheme] 

              
(eq? (list ) (list ))

            

          

        

      

    

    

      

        

          

            

              

                Scheme] 
                

              

            

          

        

      

    

    

      

        

          

            定义数据
          

        

          

            
          

        

      

    

    

      通过定义一组逻辑自洽的选择函数和构造函数，定义数据。
    

    

      比如Peano自然数公理：
    

    

      公理 1.
      .
    

    

      公理 2.
      若，则有且只有一个后继.
    

    

      公理 3.
      对任意.
    

    

      公理 4.
      对任意，若，则.
    

    

      公理 5.
      设. 若，且当时也有，则.
    

    

      

        

          

            定义自然数这种数据
          

        

          

            
          

        

      

    

    

      

        

          

            

              

                
Scheme] 

                
(define 零 (list ))

              

            

          

        

      

    

    

      

        

          

            

              

                ()
              

            

          

        

      

    

    

      

        

          

            

              
Scheme] 

              
(define (后继 x) (cons (list ) x)) 

            

          

        

      

    

    

      

        

          

            

              

                后继
              

            

          

        

      

    

    

      

        

          

            

              
Scheme] 

              
(后继 零)

            

          

        

      

    

    

      

        

          

            

              

                (())
              

            

          

        

      

    

    

      

        

          

            

              
Scheme] 

              
(后继 (后继 零))

            

          

        

      

    

    

      

        

          

            

              

                (() ())
              

            

          

        

      

    

    

      

        

          

            

              
Scheme] 

              
(后继 (后继 (后继 零)))

            

          

        

      

    

    

      

        

          

            

              

                (() () ())
              

            

          

        

      

    

    

      

        

          

            

              

                Scheme] 
                

              

            

          

        

      

    

    

      

        

          

            cons/car/cdr的其中一种实现
          

        

          

            
          

        

      

    

    

      

        

          

            

              

                
Scheme] 

                
(define (cons2 x y)
  (define (dispatch m)
    (cond ((= m 0) x)
          ((= m 1) y)
          (else (error "Argument not 0 or 1 -- CONS" m))))
  dispatch)

              

            

          

        

      

    

    

      

        

          

            

              
Scheme] 

              
(define (car2 z) (z 0))

            

          

        

      

    

    

      

        

          

            

              
Scheme] 

              
(define (cdr2 z) (z 1))

            

          

        

      

    

    

      

        

          

            

              
Scheme] 

              
(car2 (cons2 1 2))

            

          

        

      

    

    

      

        

          

            

              
Scheme] 

              
(cdr2 (cons2 1 2))

            

          

        

      

    

    

      

        

          

            

              
Scheme] 

              
(car2 (cons2 1 (cons2 2 (cons2 3 ()))))

            

          

        

      

    

    

      

        

          

            

              
Scheme] 

              
(car2 (cdr2 (cons2 1 (cons2 2 (cons2 3 ())))))

            

          

        

      

    

    

      

        

          

            

              

                Scheme] 
                

              

            

          

        

      

    

    

      

        

          

            总结