增长的阶—  记法 记法
|
|
零基础SICP:第5课
|
|
编程的基本原理
|
Elements of Programming
|
线性递归和迭代 |
Linear Recursion and Iteration |
树形递归 |
Tree Recursion |
增长的阶 |
Orders of Growth |
求幂 |
Exponentiation |
最大公约数 |
Greatest Common Divisors |
术语回顾
|
|
应用一个函数的代换模型:
应用序求值
正则序求值
递归的计算过程
迭代的计算过程
递归函数的计算过程不一定是递归的,也有可能是迭代的。
正则的英语原文是regular,可以理解为有规律的,有规则的。在英语里面被描述为regular的对象其实是比较简单的,容易掌握的对象。比如说正则语言只有几条简单的定义,除了原子(atom)的定义就是各种连接(concatenation)和求并(union),并且可以简单的用确定状态有限自动机表达;相对而言,上下文无关以及上下文相关语言就要复杂的多了,需要下推自动机和线性有限自动机来表示了。
增长的阶—  记法 记法
|
|
定义 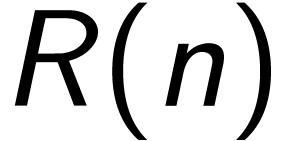 是一个计算过程在处理规模为n的问题所需要的资源量。如果存在与
是一个计算过程在处理规模为n的问题所需要的资源量。如果存在与 无关的整数
无关的整数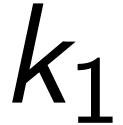 和
和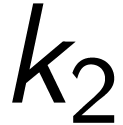 ,使得
,使得
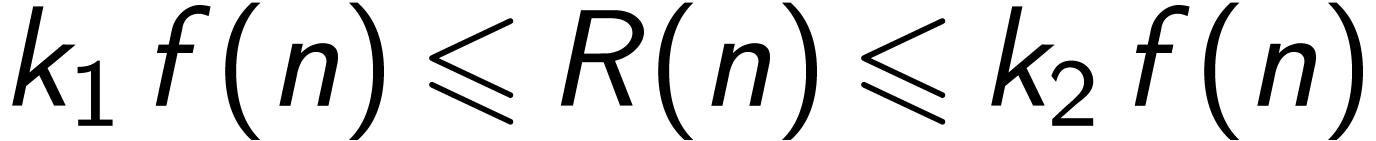
对任何足够大的 值都成立,我们称
值都成立,我们称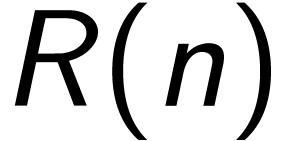 具有
具有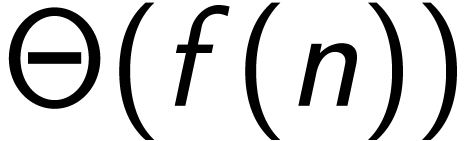 的增长阶。
的增长阶。
例 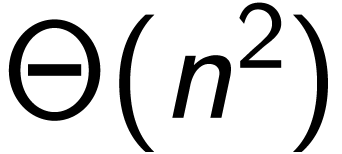
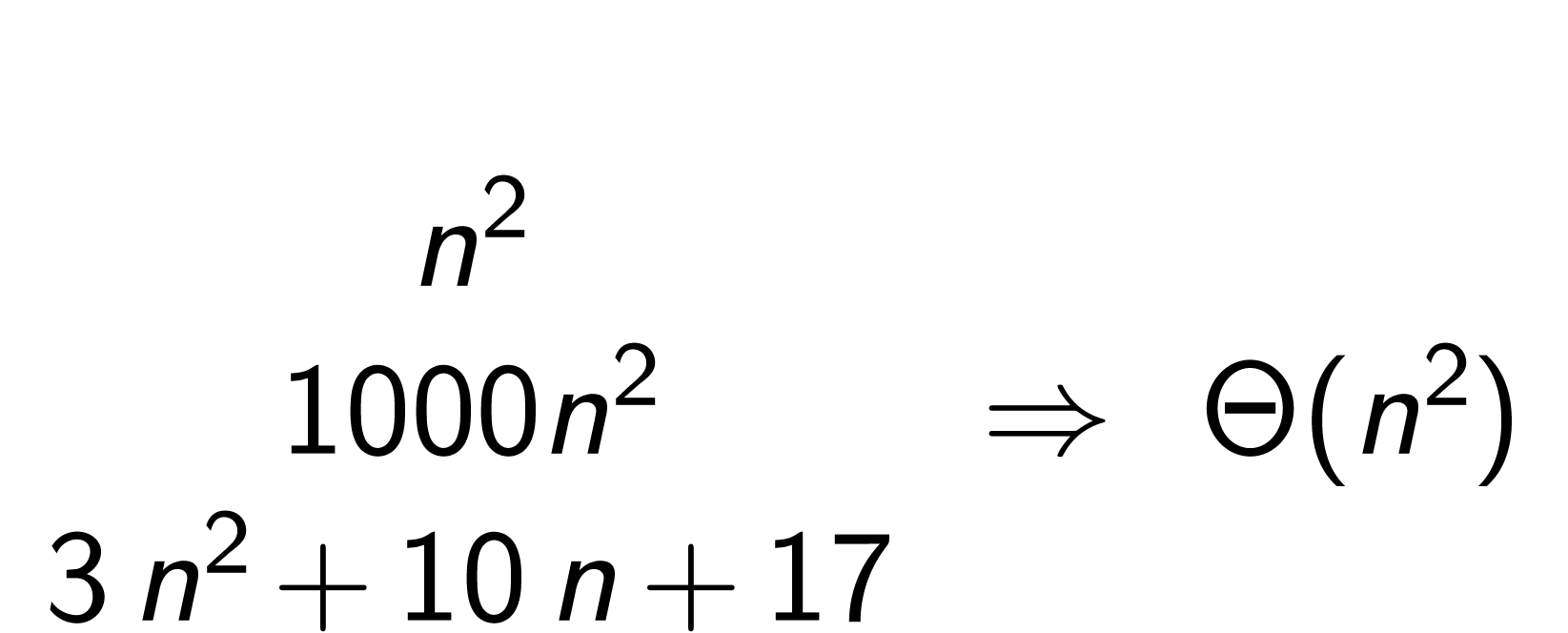
算法导论对  记号的定义 记号的定义
|
|
定义 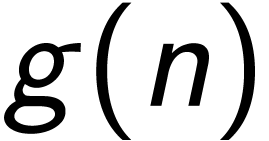 ,我们使用记法
,我们使用记法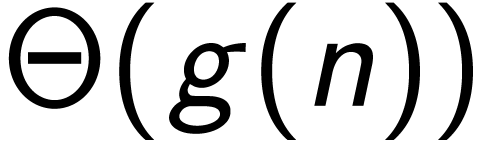 表示一组函数的集合:
表示一组函数的集合:
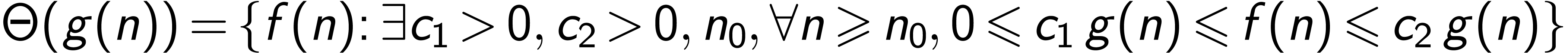
定义 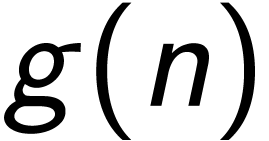 ,我们使用记法
,我们使用记法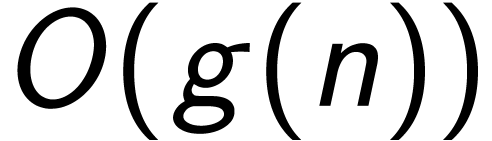 表示一组函数的集合:
表示一组函数的集合:
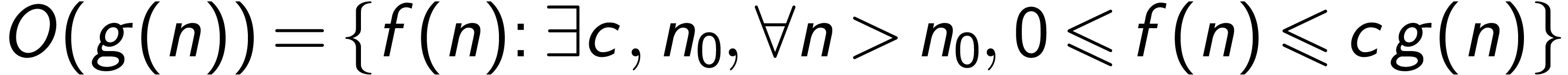
定义 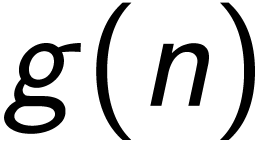 ,我们使用记法
,我们使用记法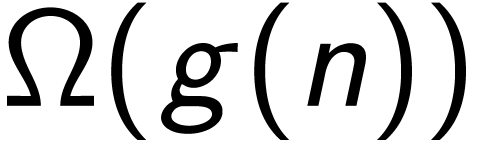 表示一组函数的集合:
表示一组函数的集合:
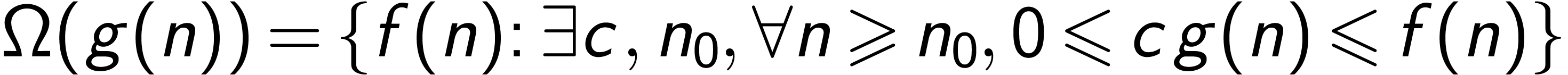
链表的定义
|
|
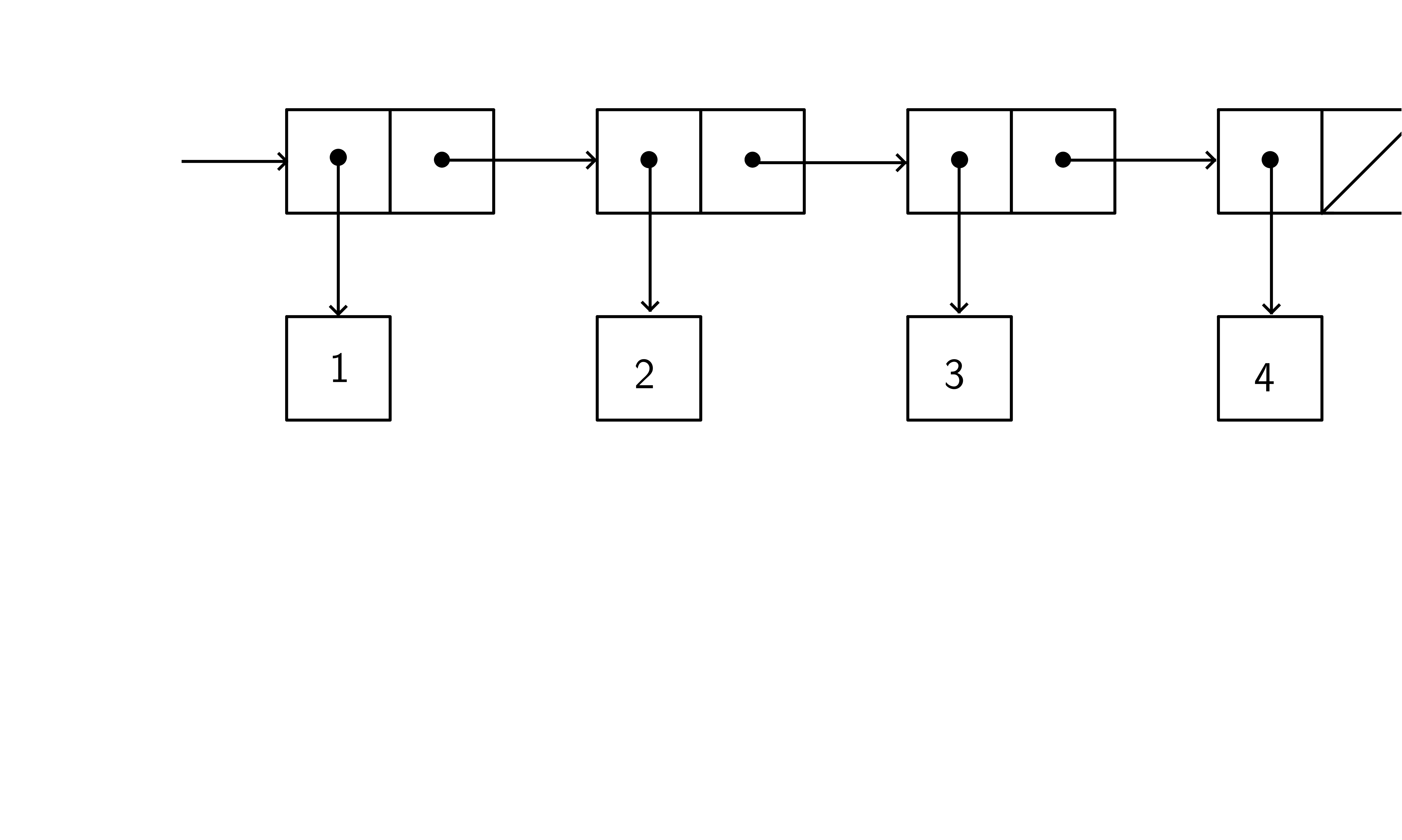
(cons 1 (cons 2 (cons 3 (cons 4 ()))))
https://srfi.schemers.org/srfi-1/srfi-1.html
Scheme] |
() |
()
Scheme] |
(list 1 2 3 4) |
(1 2 3 4)
Scheme] |
(cons 0 (list 1 2 3 4 5)) |
(0 1 2 3 4 5)
Scheme] |
(cdr (list 1 2 3 4 5)) |
(2 3 4 5)
| Scheme] |
求链表长度的时间复杂度
|
|
Scheme] |
(eq? () (list )) |
#t
Scheme] |
(define (list-length l)
(if (eq? () l)
0
(+ 1 (list-length (cdr l))))) |
list-length
Scheme] |
(list-length (list 1 2 3 4)) |
4
Scheme] |
(define (list-min l)
(if (= (list-length l) 1)
(car l)
(min (car l) (list-min (cdr l))))) |
list-min
| Scheme] |
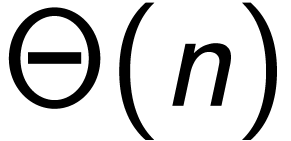
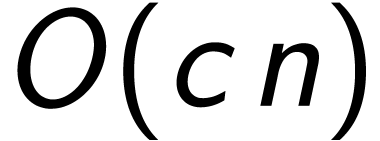
range(n)的时间复杂度
|
|
Scheme] |
(define (range n)
(define (range-iter k n)
(if (= k n)
(list n)
(cons k (range-iter (+ k 1) n))))
(range-iter 1 n)) |
range
Scheme] |
(range 3) |
(1 2 3)
| Scheme] | (define (range n) (append (range (- n 1) (list n)))) |
求幂——线性递归的计算过程
|
|
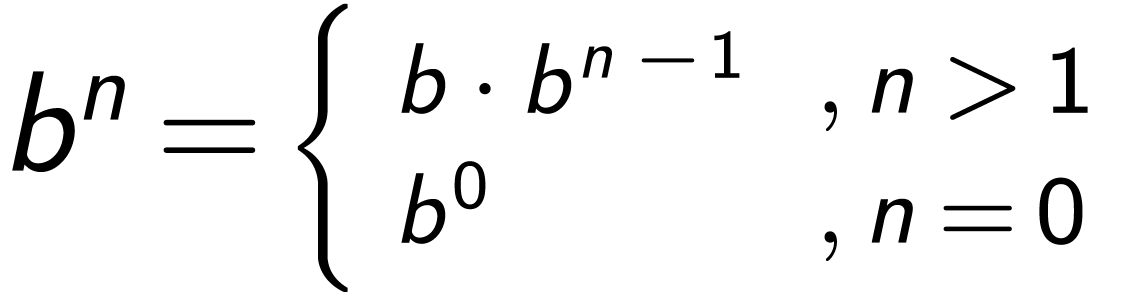
Scheme] |
(define (expt-1 b n)
(if (= n 0)
1
(* b (expt-1 b (- n 1))))) |
expt-1
Scheme] |
(expt-1 1 0) |
1
Scheme] |
(expt-1 2 3) |
8
求幂——线性迭代的计算过程
|
|
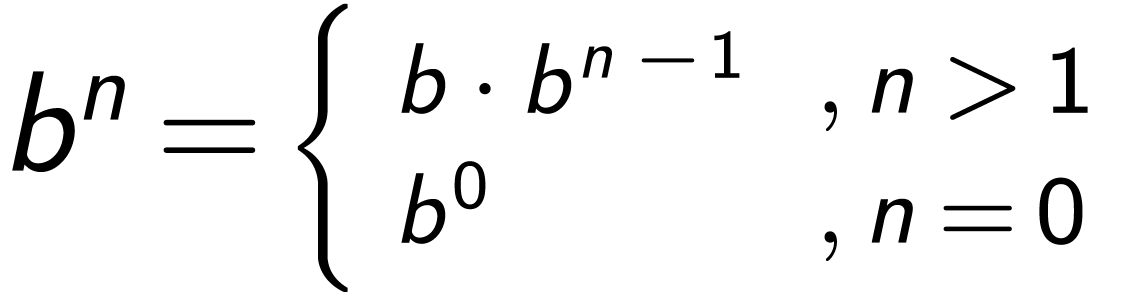
Scheme] |
(define (expt-2 b n)
(define (expt-iter b counter product)
(if (= counter 0)
product
(expt-iter b
(- counter 1)
(* b product))))
(expt-iter b n 1)) |
expt-2
Scheme] |
(expt-2 3 3) |
27
求幂——优化方案
|
|
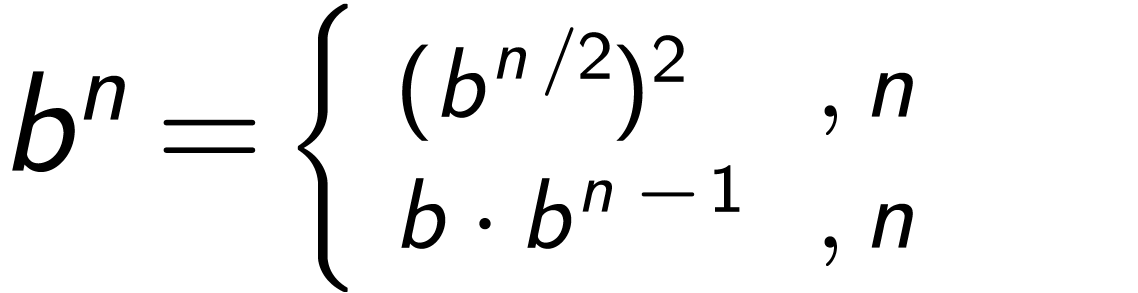
Scheme] |
(define (fast-expt b n)
(define (even? n)
(= (remainder n 2) 0))
(define (square x) (* x x))
(cond ((= n 0) 1)
((even? n) (square (fast-expt b (/ n 2))))
(else (* b (fast-expt b (- n 1)))))) |
fast-expt
Scheme] |
(fast-expt 3 3) |
27
最大公约数
|
|
Scheme] |
(define (gcd a b)
(if (= b 0)
a
(gcd b (remainder a b)))) |
这个例子的特点在于,我们不知道求两个数的最大公约数,到底需要几个迭代步骤。
练习  的证明。
的证明。
总结
|
|
术语回顾:正则是个什么鬼
时间复杂度和空间复杂度的记号
回顾在第三课提到的range函数
求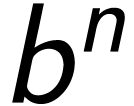 的不同实现的不同时空复杂度
的不同实现的不同时空复杂度
有一些算法的时间复杂度并不是显而易见的,需要数学去证明
斐波那契数列第n项的计算是一个树形递归,并不能很方便地转换为线性迭代的计算过程:
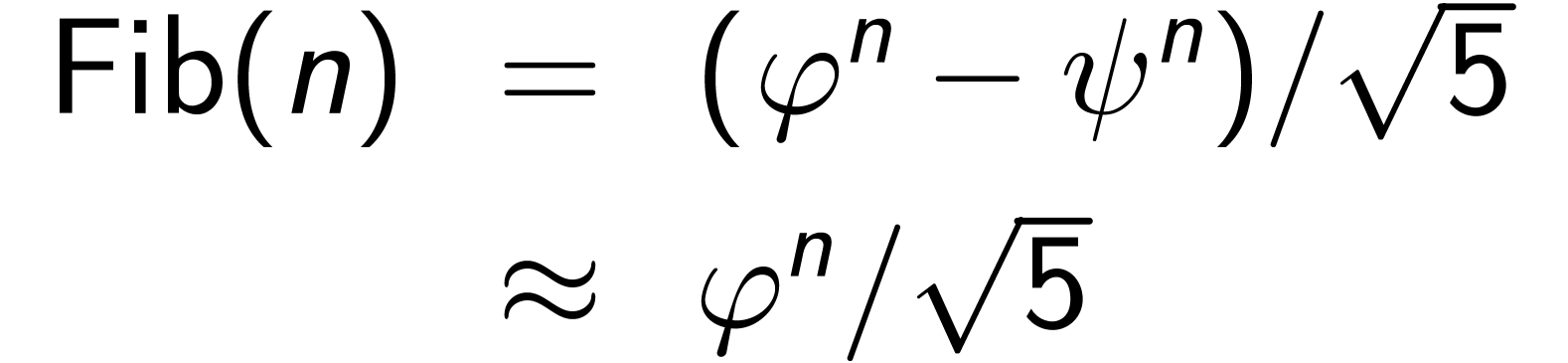
练习
思考题. 在有限的时间内,比如1分钟,得到能够计算出来的斐波那契数列最大一项。